- ユニケミートップ
- Uni-Lab(分析技術情報)
- 波の真実 ⑴ 振動のアレコレ -なぜブランコは地面に近い所で速いのか?-
波の真実 ⑴ 振動のアレコレ -なぜブランコは地面に近い所で速いのか?-

バネを引っ張って離すと上下に振動します。一方向の振動を単振動と呼びます。
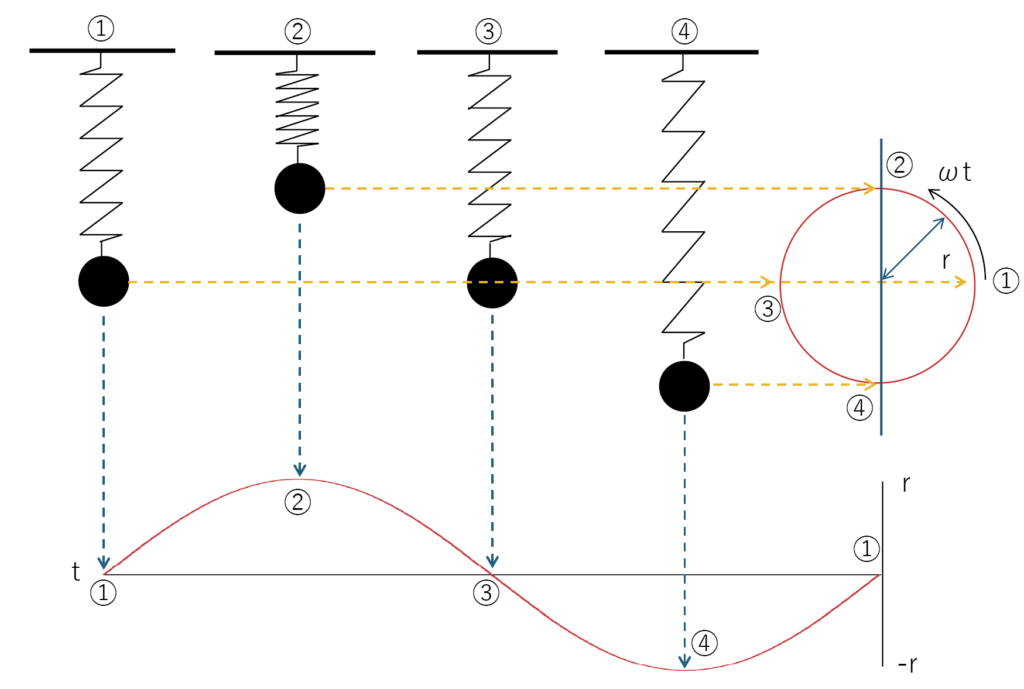
単振動では、一定の速さで円運動する点を縦軸に投影した運動と同じになります。一定の速さを角速度ωで表し、振幅は円の半径rと等しくなります。
角速度は1秒間に何rad進むという意味です。
例えば、時計の長身は12時間で1周するため角速度は、
2π/(12×60×60) rad/s
となります。
単振動を三角関数で示すと、
y=r・sin(ωt)
となります。
グラフにすると、横軸が時間t、縦軸が振幅rの波として表現することができます。
音と振動の場合は、周期を周波数fで表し、単位はHz(ヘルツ)です。
角速度ωと周波数fの関係はω=2πfになります。1Hzで円一周(2π)と覚えます。
定点で振動測定すると、複数の振動が混ざり合った波形がよく見られます。
この波形を構成する振動のrとωを取り出す作業が周波数解析と呼ばれます。
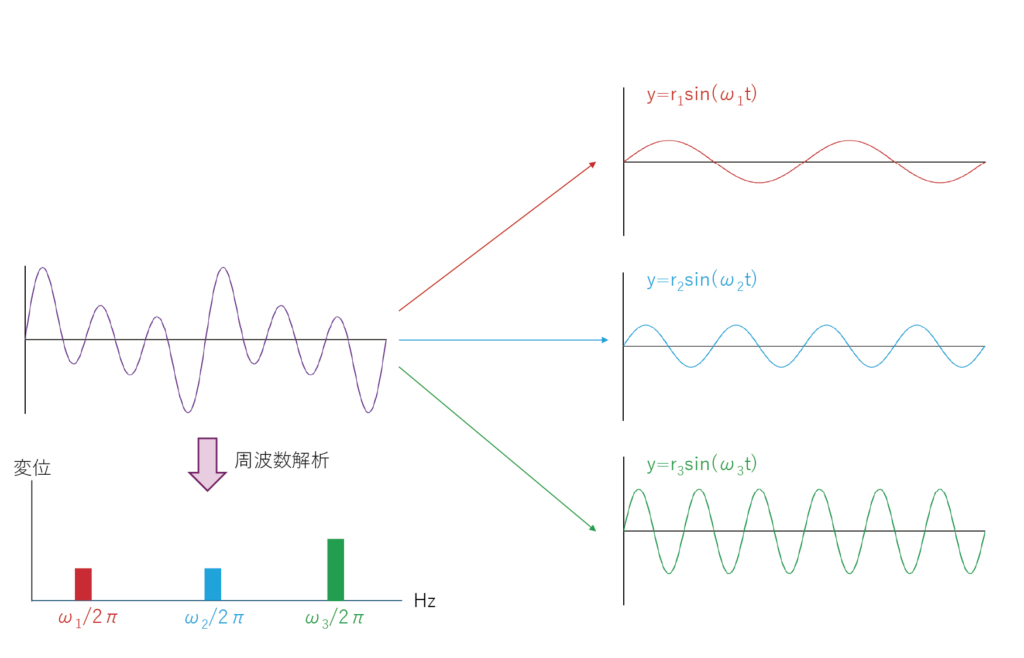
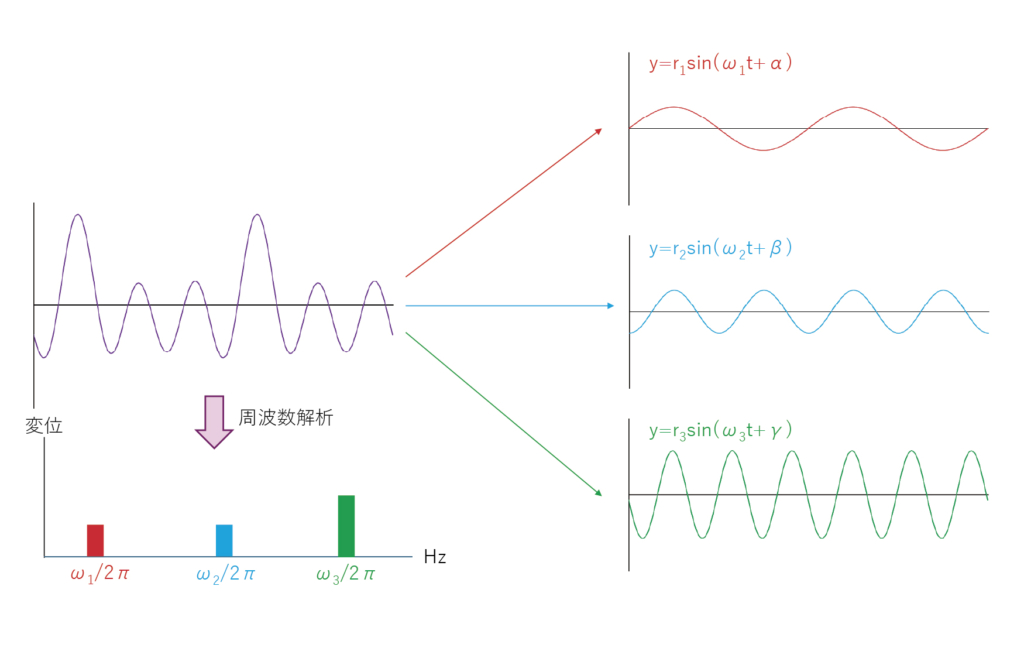
全く異なる波形の振動でも、周波数解析すると同じ結果になる場合があります。
構成する振動の位相がズレているためです。
ビリヤードの手玉が的玉に衝突したときの挙動を考えてみます。
手玉が的玉に当たると、図のような動きをします。
運動する物体が他の物体に衝突したときの挙動を式にすると、
m1・v0=m1・v1+m2・v2
と表すことが出来ます。
ビリヤードのようにm1とm2が等しい場合、例えば45°で衝突すると、v1とv2は等しくv0の半分となり各々45°の方向へ(v1とv2の間の角度は90°)運動します。
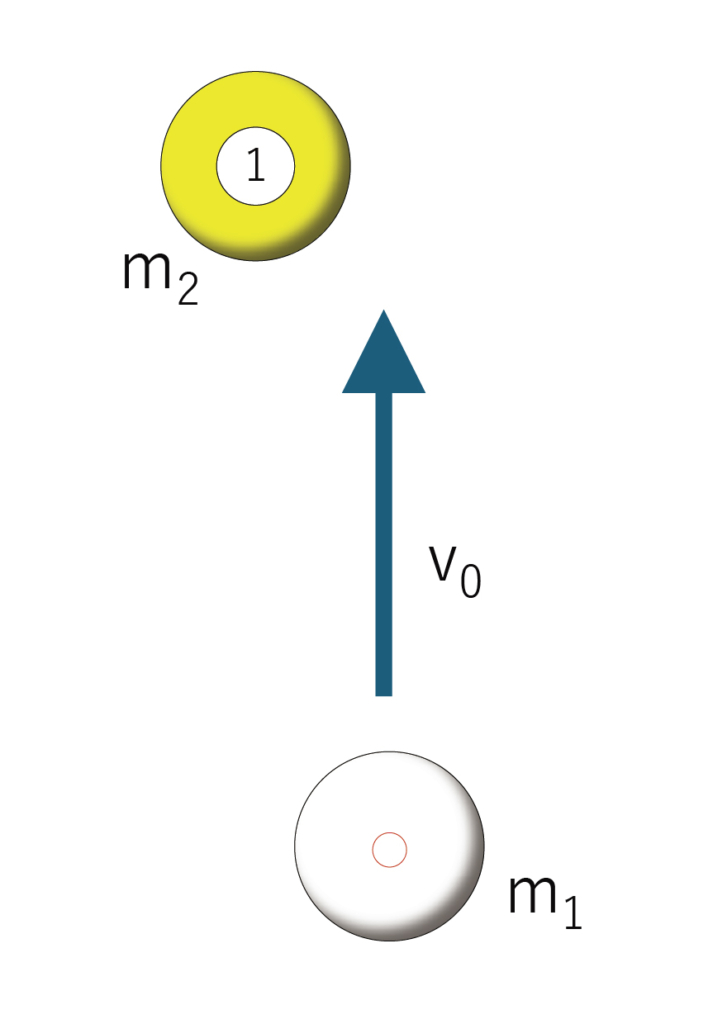
①手玉をショットする

②手玉が的玉に衝突する
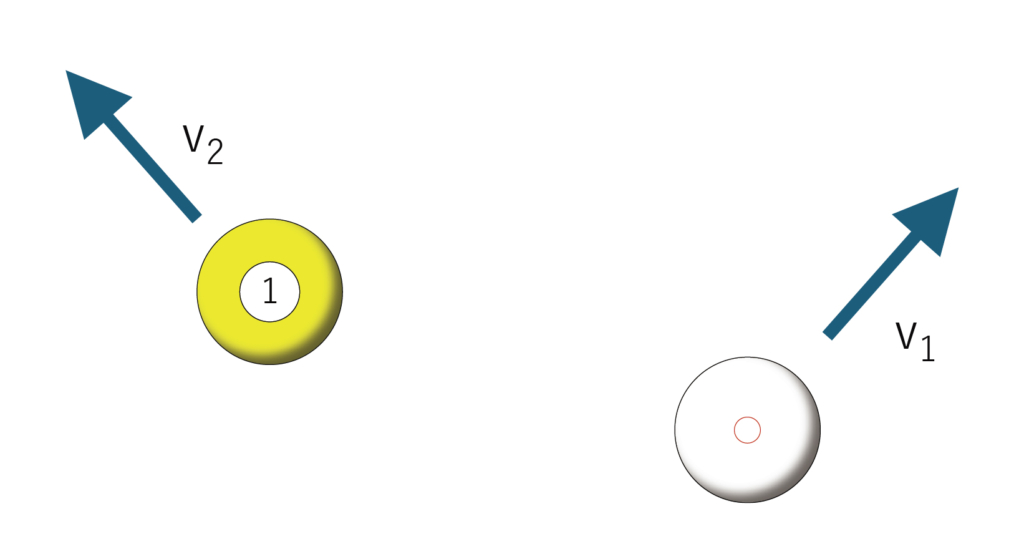
③別々の方向に運動する
ここでmは質量、vは速度を示します。
質量と速度の積を力積と呼びます。
地震など地面が振動する場合、m1が非常に重いと考えます。
そのため、振動速度が地表の対象物m2に対して大きな影響を与えます。
ビリヤードの手玉が10倍重かったらと考えると、的玉に伝わる衝撃の大きさが想像できると思います。
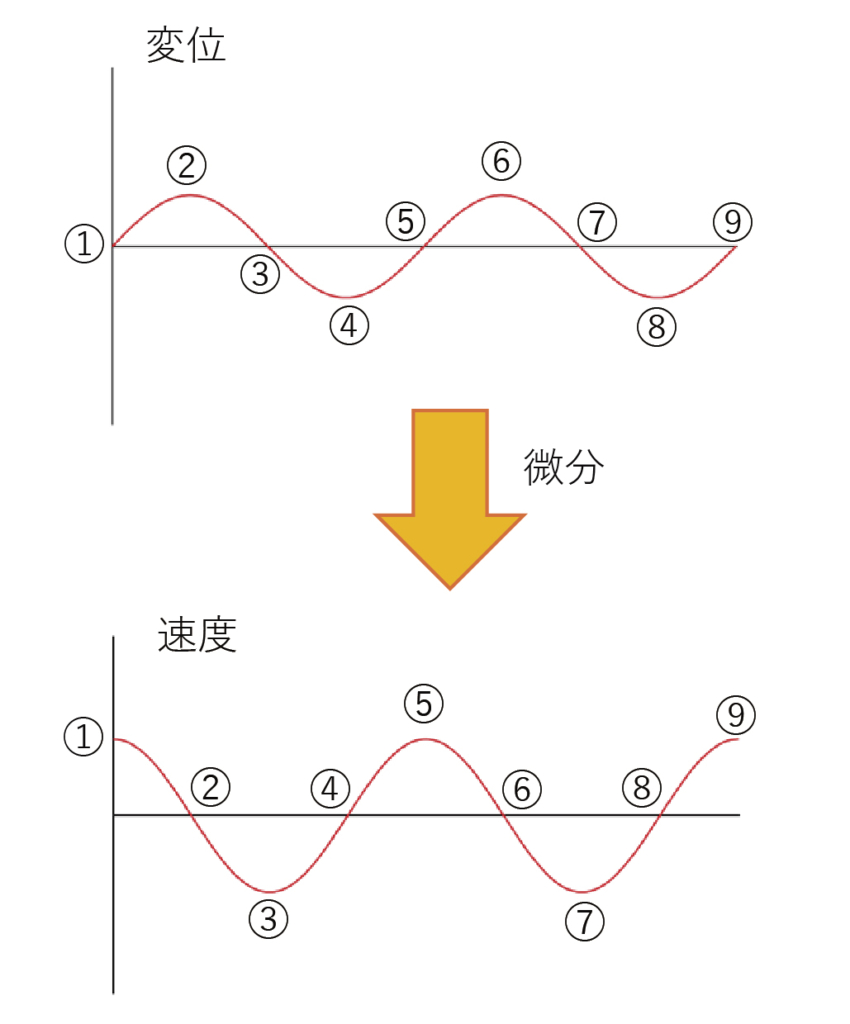
速度は変位を時間で微分して求めます。
まず、三角関数の微分を少し復習します。
y=sinθを微分すると、dy/dθ=cosθになります。
y=cosθを微分すると、dy/dθ=-sinθになります。(後ほど加速度で再登場)
微分するたびに、sin→cos→-sin→-cos と 1/4 周期 (90°=1/2 π)づつ回ります。
振幅r、角速度ωとした場合、
y=r・sin(ωt) を微分すると、速度v=dy/dt=rω・cos(ωt)
になります。 注:sinがcosに変わってωが前に出てきます。
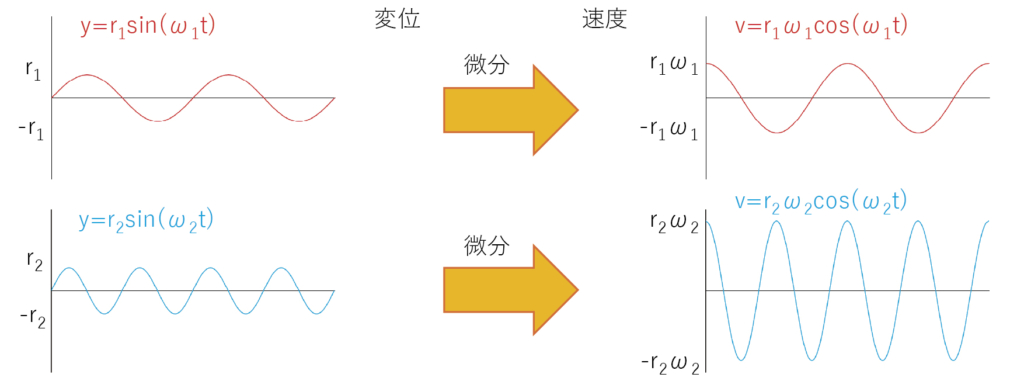
速度の最大値は、振幅と角速度の積で表されます。
振幅が等しい場合、角速度が大きい方が速度も大きくなります。
変位と速度の位相差は1/4周期なため、変位が0の時に速度は最大値または最小値を示します。
変位と速度の位相が1/4周期ズレるの?っと思った人。
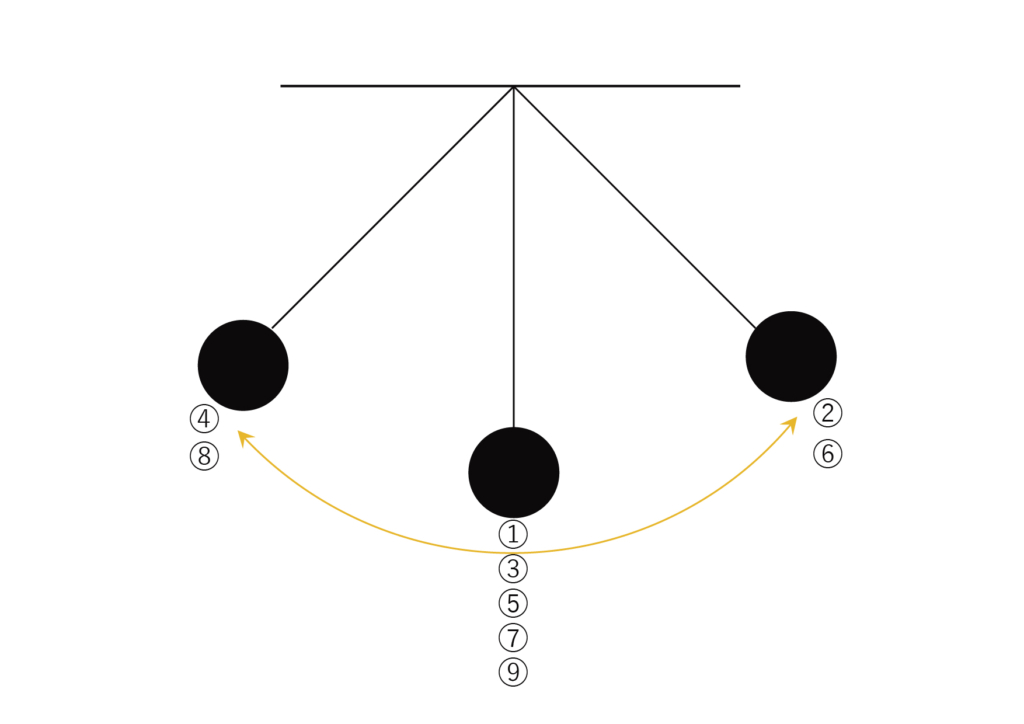
ブランコに乗ってください。
揺れるブランコで最も地面が最も近い (静止状態と同じ位置=変位0)時に、一番速くないですか?
ブランコは三角関数の微分を体感できるアイテムです。
「F=ma」物理で最も有名で、最も重要で基本の式です。
F(力)はm(質量)とa(加速度)の積と言う意味です。
次は加速度について考えてみます。
加速度は速度を時間で微分したものです。
変位:y=r・sin(ωt)
↓ tで微分
速度:v=rωcos(ωt)
↓ tで微分
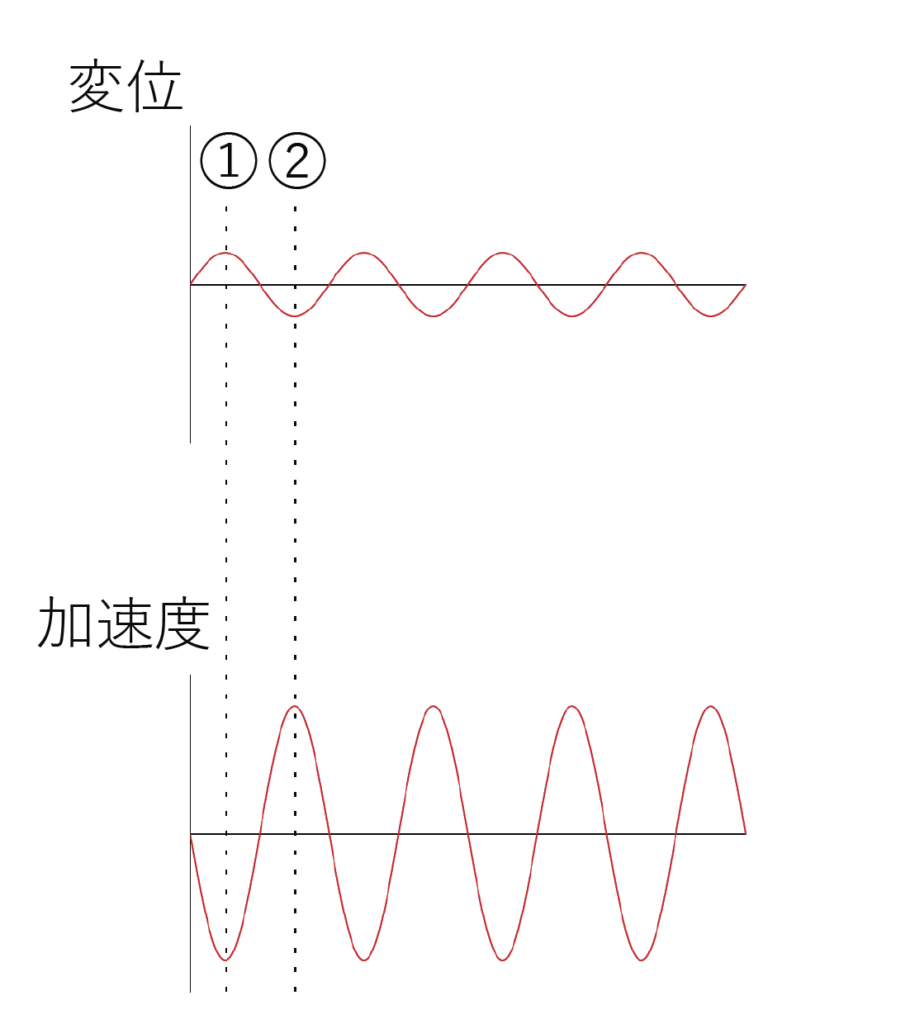
加速度:a=-rω2sin(ωt)
微分するたびに位相が1/4周期(1/2π=90°)左にズレて、ωが掛けられます。
高周波の振動や音の場合、ωが大きいため微分すると大きな値になります。
速度や加速度のマイナス側は数値が小さいと言うより、運動方向が逆と考えます。
エンジンはピストンで発生する単振動を、クランクで円運動に変換する機械です。
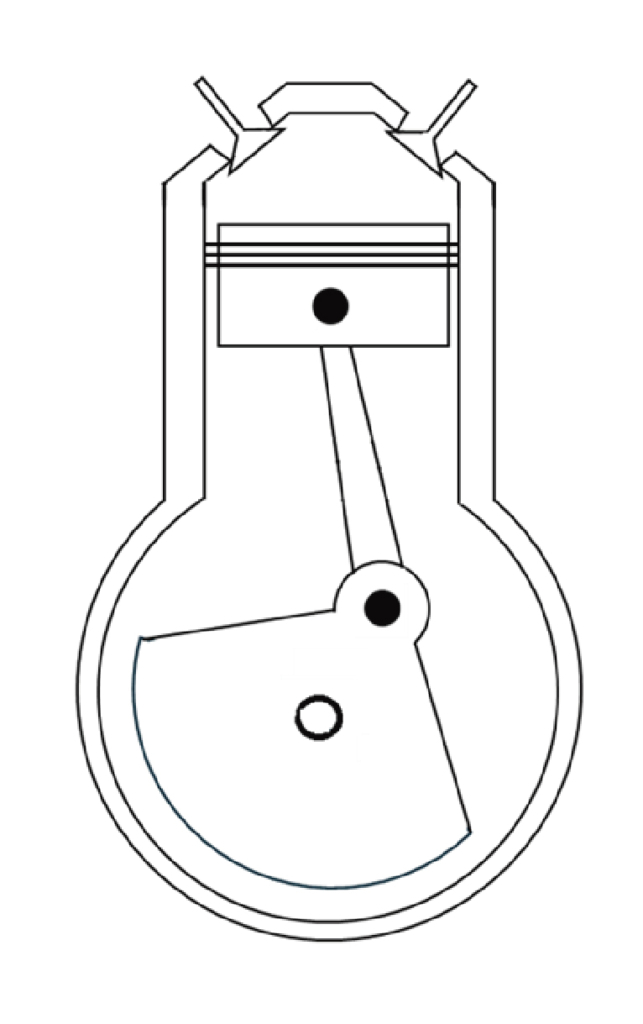
例えば、ストローク100mmのエンジンが3000rpmで回っていたとします。
ピストンの質量を50g=0.05kgと仮定します。
ピストンのストロークはクランクの直径と等しいため、半径rは50mm=0.05mになります。
rpmは毎分何回転という意味なため、角速度ωは3000/60秒×2π=100πになります。
この条件で加速度の最大値を計算してみます。
加速度:a=-rω2sin(ωt)<rω2(三角関数の最大値は1)
振幅:r=0.05
角速度:100π
加速度aの最大値は0.05×(100π)2=500π2≒4934.8m/s2となります。
ピストンにかかる力F=maを計算すると、0.05×4934.8=246.74Nになります。
力の単位N(ニュートン)ではピンとこないと思うため、重力加速度g=9.8m/s2で割って重さに換算します。
246.74/9.8=25.18kg
たった50gのピストンは、上死点と下死点で約25kgに相当する力を受けることになります。
物体に加わる力の影響を考える時、加速度は重要な要素になります。
RANKING 人気事例ランキング
-
 1
1 -
 2
2 -
 3
3 -
 4
4 -
 5
5
TAG LIST